
7. TESTING FOR VALIDITY
So far we have simply tried to distinguish deductive from non-deductive arguments, but the question of greater practical importance is whether an argument is valid or invalid, and it is to this that we shall now turn.
But the prior question (deductive or non-deductive?) is important because in the case of deductive arguments it is easy to say what makes them valid or invalid, and so fairly easy in many cases to set about testing for validity, whereas in the case of non-deductive arguments it is much harder. In this section we shall look at deductive validity; I shall say a few words about non-deductive arguments in the next section.
Let us recall what we are saying when we say that an argument is deductively valid. We are saying that it is impossible for the premises to be true while the conclusion is false. But it is essential that you see that this exclusion does not actually say anything about what the premises or conclusion are; it is, as I have stressed before, conditional - it says that the conclusion will be true if the premises are, but of course that says nothing about whether the premises actually are true. So, in fact, the deductive guarantee is quite compatible with the following cases:
And equally, the deductive guarantee may be absent from arguments with the same combinations of truth and falsity in premises and conclusions (especially (a) - the mere fact that both the premises and the conclusion of an argument are true does nothing to show that it is valid). The one combination you won't get with a valid deductive argument is premises true and conclusion false.
It is perhaps worth noting, though the problem goes too far into logical theory for us to discuss it, that this account of deductive validity allows for two degenerate cases. A valid deductive argument is such that you cannot have the premises true and the conclusion false. But one way of satisfying that requirement is by being unable to have the premises true at all, i.e. by having contradictory premises. And another way is to have a conclusion which cannot be false, such as what are called logical truths, or the tautologies we shall meet in Section 10. So we must count the following as deductively valid arguments, however useless for argumentative purposes they might be: "Grass is green; grass is not green, so snails are best in lots of garlic" (where the premises together are a contradiction) and "Lafite is very expensive, so either it is raining or it is not raining" (where the conclusion is a tautology). These cases may show you that the simplifications involved in logical theory sometimes lead to clashes with what common sense might understand by a formally good argument.
Let us return to normal types of deductive argument. Looking for validity, or invalidity, is not a matter of asking whether the premises and conclusions are in fact true or false but of asking whether they could be, in particular asking whether the premises could be true while the conclusion was false or whether that combination is impossible. Go back to the three examples above, and convince yourself that they are all such that the premise couldn't be true while the conclusion was false. If it were the case that all men spoke English, then it would have to be true that all men everywhere spoke English, wouldn't it?
It is because we don't need to know whether premises and conclusions actually are true or false that we can evaluate deductive arguments in any field. You don't need to be an expert, you just need to be able to imagine possibilities to decide whether an argument is deductively valid or invalid.
What exactly should we do to test a deductive argument? Let us take one of our earlier examples: someone argues from the premises "No communists are Christians" and "Ade is not a Christian" to the conclusion "Ade is a communist." To test this, first imagine that the premises are true - no communists are Christians, and Ade is not a Christian. Second, ask yourself whether, in the world you are imagining, it could be false that Ade is a communist. Well, there are endless possibilities - Ade might be an anti-communist Zen Buddhist, or there might be no communists at all, just Christians and Muslims, or .... What does this show? It shows that it is possible for the premises of the argument to be true and the conclusion false; that is to say, it shows that the argument is invalid, it lacks the deductive guarantee it was pretending to. The argument is no good; it does not achieve what it tries to achieve. Perhaps Ade is a communist; still this argument does nothing to support that claim.
Let us pause a moment to see exactly why that last claim is true. Think of yourself as on an island in a river where there are many other islands and quite a few stepping stones between them. You may then imagine asking yourself the question: can I get from where I am to that island without getting wet? Is there a path or not? You can see the premises of an argument as the stepping stones to the island, the conclusion, you want to reach. Now if you've got a valid argument with true premises, you have got such a path. But there are two ways you can go wrong. What you thought was a stepping stone is just an illusion: this is like having a valid argument with a false premise. But again you might have a lot of stepping stones but they don't reach where you want to go: that is the situation we met at the end of the last paragraph - even if the premises and the conclusion are true, these stepping stones don't take you to that island.
What we try to do to test a deductive argument is to find what we may call a counter-example to it - a case where its premises hold but its conclusion is false.
So far we have been looking for counter-examples with just the argument itself which we are testing. In a way this is the safest procedure, but there is a practical obstacle: people tend not to think very hard when they already know that a claim is true or false. I was just using the name, "Ade", for the sake of the example, and possibly you haven't been thinking of anyone in particular; but if I had used the name "Andropov" (now that the Russian gerontocracy are dropping like flies, you must think of whichever prominent Russian communist you know) you might have been much more willing to accept the validity of the argument because you know already that Andropov is a communist. And if by now you wouldn't have given up searching for counter-examples, let me assure you that the evidence is that ordinary people who have not been exposed to training in logic certainly would have. So what can we do instead?
There are two strategies, or rather two variants on the same basic strategy, that you can use to get away from the distraction of the actual claims in the argument you are testing. To understand them you have to understand, or at least be able to handle, the notion of the structure of an argument or of a statement. We have already looked at the structure of arguments at one level, but now we have to go somewhat closer to the component premises and conclusion and often inside the various sentences used to express them. I shall not try to say much explicitly about structure here, but hope that you will be able to pick it up from some examples. One useful question to ask concerns what other words can be substituted for a word or phrase in a sentence: such substitutions will often yield instances of the same structure. Thus "Ade is a communist", "Andropov is a communist", "Natasha is a communist", are all clearly examples of the same sentence structure. Again "Ade is a communist" and "Ade is a Muslim" exemplify a shared structure, while at a more abstract level of structure "Ade is a communist" and "John is a Christian" belong together. Of particular importance for the analysis of arguments are the structures created by little words that join whole sentences together (in grammar, the sentences are often called "clauses" after they have been joined together), words like "if...then...", "either...or...", "...unless..."; and also the word "not". Yet another crucial set of words are those that tell about how many: "all", "no", "most", "some", etc. With these as cement, and the vast resources of the vocabulary as bricks, we can build an unlimited number of sentences out of a limited number of basic structures. And luckily for us, questions of the validity of deductive arguments are usually answerable by looking, not at the particular argument with its particular bricks, but rather at a structure that it exemplifies.
The two variants of the appeal to underlying structure are either to take the original argument and replace some of its constituent bricks so as to yield another argument of the same structure, with the same pattern; or to move to an abstract level in which mere letters stand for the bricks. To illustrate with our premise that no communists are Christians: we could make some substitutions so that it becomes "No insurance salesmen are vegetarians," or we could go straight to the level of structure that is relevant by transforming it into "No As are B." If you are especially concerned about religion or communists, changing the argument to one of the same form about vegetarian insurance salesmen may allow you to test it more carefully; if you'd rather not try to imagine such weird substitutions and are happy talking about As or ps or xs, then going straight to the abstract structure may be easiest. Either way, your job is still the same - to construct, if you can, a counter-example to the argument. But now, instead of the original argument, you are directly testing either another argument of the same structure or the structure itself.
It is because of this shift from the original argument to its structure (either examined directly or through an analogous substitute) that there can be a residual doubt about such testing. Did you find the right structure? Arguments, and statements, can be analysed into structures at different levels and in different ways; so you may always wonder whether you have captured enough detail of the original argument when you test it by appeal to a structure it exemplifies. Practice gives you a fair idea of the dangers here, but it is always worth going back to the original argument to see if your proposed counter-example will work in that context.
So far we have looked at the technique of looking for a counter-example to an argument. If we find one, this tells us that the argument, or the argument-structure in question, is deductively invalid; those premises do not entail that conclusion. But how about a direct test for validity? And what can we infer if we can't find a counter-example? To answer the second question first: we cannot be certain of anything if we fail to find a counter-example. It may be because there cannot be a counter-example (if the argument is valid) or it may be because we have simply not been lucky enough to think of a counter-example that does exist. Looking for counter-examples tells us an argument-structure is invalid if we find one, but it tells us nothing if we don't.
So how do we tell that a structure is valid? In simple cases we can simply "see" that an argument structure is valid, that you couldn't have its premises true and its conclusion false. If all men are mortal and Socrates is a man, then Socrates has got to be mortal, hasn't he? Any attempt I might make to convince you of this is likely to be less convincing than the original argument appears. But people are rightly suspicious of what people (especially other people) claim to be able to see as so obvious, and it is not difficult to produce short and simple argument structures about which our intuitions are by no means so reliable. So we should like ways of testing for validity that are not so inscrutable. They exist, but to examine them properly is beyond the scope of this booklet. I shall, however, indicate three general strategies which we can use.
For some kinds of argument (some of those crucially dependent on "all", "no", "some" or even "most") we can draw diagrams that model the premises of the argument. You then look to see whether all the possible diagrams for the premises already contain the diagram for the conclusion - if so then you can't have the premises true without the conclusion true as well, so the argument is valid; if not then the premises do not force the conclusion upon you. There are various ways of using diagrams here; one of the commonest, due originally to Euler, involves circles - "All A are B" requires you to draw a circle for the As inside a circle for the Bs; "Some As are B" has the two circles overlapping; "No As are B" has the two circles quite separate from each other; "Some As are not B" has again two overlapping circles, but the focus is on the bit of the A circle outside the B circle. There are some problems with this way of drawing the various claims, but with care it allows a very simple approach to a good number of arguments.
To see it in action, consider this somewhat strange argument: all boys are human; some humans are male; so all boys are male. Remember we are testing the argument as given. We first draw a diagram of the first premise: a circle for the boys inside a circle for the humans, thus:

Then we add a diagram for the second premise, which means that we must draw a circle for the males overlapping that for the humans, thus:

In this diagram, the circle for the boys is still inside the circle for the males, which is how the conclusion say things are; but we could equally well have drawn the third circle differently, thus:

That diagram pictures everything we are told in the premises but we don't find the boys inside the males, so we could have had the premises true but the conclusion false, so the argument is invalid. Notice as before, you have to ask yourself about possibilities; stopping with the first three-circle diagram would have given the wrong answer.
Suppose the second premise had been "All humans are male." Then we would have had to draw the male circle around the human circle, thus:
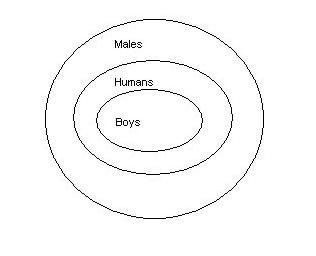
Check for yourself that there is no other way to draw the premises in this revised argument. In this case, the way the premises are drawn forces us to accept the original conclusion since we cannot draw them without at the same time having the circle for the boys inside the circle for the males. The revised argument is thus seen to be valid, however unlikely the premises.
Circles and other diagrams can be very helpful for some simple arguments, but they have their limitations, especially when we consider differently structured arguments or arguments with many components. A different strategy is to start with a few simple, intuitively valid argument forms as your only allowable moves, and then try to find a route from the premises of your argument to its conclusion using only these simple and obviously valid steps. This approach is often called "natural deduction" since it is fairly close to what we would ordinarily do in trying to explain an argument for the benefit of someone who didn't follow it. Instead of simply repeating the argument, we might well try to fill in some of the gaps, try to make the steps shorter and more obvious. Suppose you argued: if John is winning, Mary is happy; and if Mary is happy Tom doesn't cry; but Tom is crying so John isn't winning. Now if your audience didn't follow, you might expand it thus:
- (40) If Mary is happy, Tom doesn't cry;
- but Tom is crying,
- so Mary isn't happy;
- but if John is winning, Mary would be happy,
- so John isn't winning.
Here you have spelled out the steps in the argument more fully; you are claiming that each little move you are making is obviously safe, so the whole transition from premises to your original conclusion is safe too. This is a fairly simple example, but the technique is very powerful and can be used to test very complex arguments. All you need are a set of basic patterns of argument, and ingenuity, since in general you have to discover a route from the premises to the conclusion. If you find one, the argument is valid, but if you don't, it may again only mean that you haven't been lucky.
The third strategy is very much like our first suggestion that we look for a counter-example, but with some help from the second type of strategy as well. The first approach was to ask: can you imagine the premises true and the conclusion false? If you could, the argument was invalid. Now we play the game with a slight difference - we add the opposite of the conclusion to the premises and see what happens (using some simple rules of inference as in the second strategy). The basic idea is an appeal to reductio ad absurdum since if adding the opposite of the conclusion to the premises leads to contradiction, the premises require us to assert the original conclusion, they cannot be true with the original conclusion false, which is to say that the original argument is valid. Let us see this in action on the same little argument above: add "John is winning" to the premises; then you can infer that Mary is happy, and then you can go on to infer that Tom isn't crying, but another of your premises is that Tom is crying, so you have arrived at a contradiction, so you can't add "John is winning" to the premises, you are forced to the original conclusion that John is not winning. This, then, is the appropriate thing to try if you can't find a counter-example to your argument - give yourself a counter-example and see if it leads to contradiction. If it does, your original argument is valid.
EXERCISE F
Look carefully at the following arguments and decide whether they are deductively valid or invalid. Try out the different suggested methods of testing, as far as you are able.
1. If the brakes failed there would be no tyre marks on the road; there are no tyre marks on the road, so the brakes failed. [Answer.]
2. All Christians are allowed to eat pork; no Muslims are allowed to eat pork; so no Christians are Muslims. [Answer.]
3. Acceleration is the second derivative of distance against time. Acceleration is an absolute quantity, so distance and time are absolute quantities. [Answer.]
4. If we devalue, prices will rise, so if we don't devalue, prices won't rise. [Answer.]
5. Horses are animals. Therefore, all horses' heads are animals' heads. [Answer.]
6. Everything is such that there is a time when it does not exist, so at some time there is nothing in existence. [Answer.]
7. Most Swedes are Protestants; most Swedes who visit Lourdes are not Protestants; so most Swedes do not visit Lourdes. [28] [Answer.]
A Note on Symbolism
I said I hoped you would pick up the idea of structure from some examples. In fact, studying logic usually rests on an assumed familiarity with a natural language (in our case, obviously, English). Thus earlier when I wrote "No As are B" I assumed you would see that this could be transformed into "No communists are Christians" or "No dreamers are people who will achieve much" but not into "No swans are fly." All you need is to be able to tell what is grammatically English and what isn't. But it certainly helps if you can explicitly pick out things like nouns and verbal phrases and so on.
Symbolism is something we choose, and people can make different choices, but some symbol systems make life easier than others. The important thing about the symbols I shall use is that they will tell you what their grammatical role is, at least for those of you who can pick out such roles. In this respect they differ from ordinary English words. As we shall have occasion to notice the word "need" may be a verb or a noun. The word "round" may belong to almost all the major word-classes. That is to say, these words may be performing very different functions in different sentences although they are written alike in all of them. A good logical symbolism refuses to let that happen.
In this book we shan't use much symbolism, but I shall try to abide by the following rules. I have already used little letters from the start of the alphabet to stand for particular sentences. When I want to refer to structures made up of sentences, but without putting in definite sentences, I shall use little letters from "p" onwards (so, "If p then q" is the structure exemplified by "If it rains (then) we shall stay at home" and by countless other sentences). The only other little letters I shall use come from the end of the alphabet ("x" onwards) and their meaning is perhaps a little complicated. Consider a sentence like "Socrates is wise." As far as logic is concerned it is made up of two bits: a name, "Socrates", and a verbal phrase, "is wise" which in logic we call a "predicate". I shall write predicates in English, but we can drop the name and replace it by a little letter to produce "x is wise." While this would give us a way of generalizing about this sort of subject-predicate sentence, its real use for us is that we can also add to it logical items such as "for all x", or "for some x" to produce sentences like "For some x, x is wise," which you should see as pretty close to ordinary English "Something is wise."
Besides these three sorts of little letter, I shall also use a variety of capital letters when employing a more traditional account of structures. I have just briefly explained one way of translating "Some men are wise" into logical notation ("For some x, x is a man and x is wise"), but it is obviously quite a big jump from the English to the logic. We can keep a lot closer to the English simply by replacing the "men" and the "wise" by capital letters, "Some M are W", as we have been doing in the previous section. Grammatically, these capital letters can be replaced by noun phrases, such as "communists", "man-eating fish", "occasions on which litmus paper turns red", or, at a pinch, "Socrateses" depending on what is grammatical in each case. There is no further restriction on which capital letters I use on any occasion.
In all cases I leave the logical words, the words that provide the logical structure, in ordinary English, although their meaning may be somewhat tightened up.
8. A NOTE ON NON-DEDUCTIVE ARGUMENTS
In the previous section we have looked at what validity means and how to test for it in the case of deductive arguments. Unfortunately in the case of non-deductive arguments these are both much more obscure and difficult questions to answer, and in this course we cannot even begin to look at the logical issues that arise. Even so, I think we can note a couple of points that might help in dealing with such arguments.
One preliminary point is that there are very many different sorts of non-deductive argument, and there is no guarantee that what is true of one sort will be true of another. Thus, on the face of it, the sort of argument exemplified by "Most students find logic difficult, Jane is a student, so Jane finds logic difficult" does not look much like arguments from evidence to a conclusion in science or history, and whereas the former type may seem to rely on relative proportions the others are not so easily cast in that mould.
For deductive arguments we have seen that the question "Do these premises support that conclusion?", in other words, "Is it a good argument?" divides into two questions - "Is the argument valid?" and "Are the premises true?" These are two separate questions, but if the answer "No" is received for either of them, then the argument in question fails in its task of giving us a good reason to believe its conclusion. The notion we started with, of support, that we pictured with the arrows in the structure diagram, has revealed itself as a composite of validity and truth, but there is a sense in which when we concentrate on validity the arrows are still going the same way. One of the things I want to suggest about a lot of non-deductive arguments is that when we dig into the notion of support, the arrows turn around, as it were. But before I try to explain this obscure remark, let us note that the other question we have distinguished, "Are the premises true?", remains as important as ever in non-deductive arguments. If you offer me scientific evidence, or historical evidence, for a certain conclusion then the support you have given to that conclusion is lost if it turns out that your evidence is a lie. I have tried to show how it is that anyone can challenge the experts simply by appeal to the logic of their arguments, but that still leaves us with having to find out which claims actually are true, and so with a need for experts in many fields.
Let us recall a couple of typical non-deductive arguments from science and history that involve the offering of evidence for a conclusion. Example (13) gave two reasons for thinking that a large chunk of the Appalachians had been transported over the eastern continental margin of North America; example (II, 5) in Exercise B gave various reasons for thinking that there had been an increase in road traffic in the Balkans in the late 16th and early 17th centuries. Let us suppose that the various claims offered as evidence are true. What, if anything, makes them into valid non-deductive arguments for their respective conclusions? We can no longer ask "Could they all be true and the conclusion false?" because that is always a possibility with non-deductive arguments - that's what makes them non-deductive. One part of the answer, but not all of it, can be seen when we note that the conclusions explain the evidence offered - this is what I meant by saying that the arrows are reversed: the argument moves from evidential premises to a conclusion, but its being a good argument requires that we can turn around and see the conclusion as an explanation of the evidence. But that is not all: we also need the evidence to be less expected in the absence of the explanatory conclusion. The conclusion must explain something that otherwise needs explanation; if we expected it anyway, it hardly helps the conclusion.
I have suggested that what often makes a non-deductive argument a good one is that its conclusion can explain its premises when they report facts that stand in need of some explanation. If this is so, there is another close link between the two kinds of argument in as much as very many explanations involve a deductive link: you can deduce the things to be explained from what is offered as their explanation. So one might almost hope that these kinds of non-deductive argument will turn into deductive ones when you exchange the premises for the conclusion. Of course, things do not work so simply in real life, but I think you can see that at least in the geological example one might hope to be able to deduce from the conclusion (that rocks had been transported over the continental margin) both that they would be highly deformed metamorphic rocks and that they would be older than the underlying strata. To do so properly one would need a good deal of geological theory and some other facts about the prehistoric situation, but in principle it would seem possible.
One reason for mentioning the intricacies of non-deductive arguments is that what I have said leads on to a useful type of challenge to such arguments. A good example of this sort of non-deductive, evidence-giving, argument requires its conclusion to explain evidence that is otherwise more difficult to explain. More difficult to explain than how? Than by appeal to what we know already and to other possible explanations. And that is the useful challenge - is there a better explanation of the evidence to be found?
Going along with such a challenge we need also to take care what our evidence actually is. Suppose someone argues: "The crime statistics are lower so economic conditions are getting better." It is very tempting to suppose that the evidence here is that crimes are being committed less frequently and that this evidence is being used to support a claim about economic conditions. But we should hesitate; what is being used are the official crime statistics, they say that crimes are being committed less frequently. We must ask why that should be; what would explain such a report? One thing that would explain it is that in fact it is true; but perhaps an equally good explanation would be that since the economy is so bad the police cannot afford to go looking for criminals or make records of reported crimes.
Without going further into the question of what is involved in explaining something, and without probing into the logical structure of non-deductive arguments, we can at least say that for one important variety, those that offer evidence for a theory, hypothesis, historical claim, etc., a good argument requires that the conclusion both explain the evidence and explain it better than plausible alternatives (particularly our previous background knowledge of the topic). The evidence must stand in need of explanation in some way. Thus in example (13), the finding that the surface rocks are older than the underlying rocks is certainly odd; it calls out for explanation in a way that perhaps the other fact, that they are deformed metamorphic rocks, does not; and it is explained by the claim that they were moved over the sedimentary rocks beneath. If the surface rocks had not been moved in this way, one would not have expected them to be older than the rocks beneath - I think the way the passage is written brings out the crucial importance of the relative ages, compared to which the deformed metamorphic nature is much less important. Again in the historical example, while Braudel admits that each individual item could be accounted for without a general increase in road transport, that becomes the only way of tying them all together and explaining them in a simple, unified way. Without an increase you might have expected some of the things he mentions, but you would hardly have expected all these things together.
Two questions to ask of a non-deductive argument of this type are: "What exactly are the data to be explained?" and "Are there any more plausible alternative explanations?" Asking such questions will, I hope, save you from some of the illusions of the epoch.
9. CRITICISM AND COGNITIVE CHANGE
Now that we have seen a little of what is going on in argument or the giving of reasons, it might be useful to suggest how we should use arguments in revising our beliefs. As we noted at the start, arguments or reasons are typically offered in order to convince you of some conclusion - that you should believe something or that you should take action of a certain sort. We have spent some time examining how to evaluate arguments. What can we say now about when and what to accept after we have evaluated an argument?
First we can rehearse the points made in Section 2. Schematically, evaluation or criticism of an argument goes as follows. Someone puts up an argument: Premises (P) Support (A) Conclusion (C).
Criticism of P is a matter of saying the premises are false or unacceptable. Even if that criticism is correct, there may be nothing wrong with A or with C, though the argument in question can no longer be used to support C.
Criticism of A is a logical challenge to the effect that this kind of argument does not give the kind of support to its conclusion which it pretends to. The conclusion doesn't follow from the premises, or the evidence isn't good enough to allow us to prefer this conclusion. Even if this criticism is correct, there may be nothing wrong with P or with C, though the argument in question can no longer be used to support C.
Criticism of C is again a matter of saying that it is false or unacceptable. If that criticism is correct, there may be nothing wrong with A, but if there isn't, and if the argument is the sort we have called "deductive", then you know that there is something wrong with at least one of the premises in P. But in other kinds of argument there may not be anything wrong with P either.
An arguer typically intends you to accept the conclusion of her argument. If you do not wish to do so, your full strategy is (i) to attack her argument by attacking either P or A or both; (ii) to produce an argument for your own conclusion. If you only do (i) you haven't undermined C itself, though you have undermined her argument for C; if you only do (ii) we are left with one lot of reasons for one conclusion and another for a different one, and so we haven't resolved the dispute. Of course, if you do (ii) when the original argument is deductive then you may be well on the way to doing (i) by attacking some part of P.
There is also the possibility that you do not want to accept the argument for C, while being happy to accept C itself. Here again, however, you have two jobs to do. You must show what is wrong with the argument, which will involve you in attacking P or A, and then you must produce your own argument for C.
So far we have considered argument as a mutually beneficial dialogue, and we have looked at the different moves separately. If you want to see the situation simply in terms of what changes you should make in your own beliefs when an argument is offered, I suggest the following simplified picture. In Figure 1, I have offered you a flow chart for argument evaluation and subsequent acceptance of claims. It presumes you start out with a consistent set of beliefs, and are then faced with an argument: Premises (P) Support (A) Conclusion (C). I think the chart gives you the quickest route to any revisions you should make.
First, you ask whether the argument is valid. If it isn't, and if you haven't got any other arguments that bear on C, then you make no changes. If the argument is valid, then you should find that you need to accept some new claims. You may notice, however, that nowhere are you told to accept the premises of the argument offered. This is because no argument can give you reason to accept its own premises - you may already accept them, but that is another story. There are three other points to notice. One is that if you are unable to judge whether to accept P or C, you are told to check that you really understand what these claims are saying. We shall be going on immediately to see some of the problems that can arise with what appears at first glance to be perfectly ordinary language.
The second point is that when you have evaluated the argument you are dealing with, the next question is whether there are any other arguments that bear on its conclusion. This connects with the point I made in the last section about alternative explanations. It is unfortunately very common for people only to examine one argument on a particular topic and to base their acceptance or rejection simply on that argument, instead of actively searching for other reasons for taking or refusing that stand on the question.
The third point is to note that the question of whether an argument is deductive or not does not appear to be very important - it seems only to arise if you don't know whether to accept the premises but do know that the conclusion is false. But this is somewhat misleading since the very first question is whether the argument is valid, and to answer that you must decide what sort of argument it is.
FIGURE 1: FLOW CHART FOR REVISING BELIEFS
- --------------
- | START: GIVEN |
- | P ---> C |---------<------
- | A | |
- -------------- |
- | |
- |
- N Y |
- ------------<-------< IS A VALID?>-->- |
- | | |
- | |
- | |
- | N IS P TRUE/ Y |
- | ------------<---------- ACCEPTABLE? --->-- |
- | | | |
- | | | | |
- | | DON'T KNOW | | |
- | | | | |
- | | ----------------- | |
- | | | CHECK YOU | | |
- | | | UNDERSTAND P | | |
- | | ----------------- | |
- | | | | |
- | | | |
- | | Y IS A N IS C TRUE/ Y | |
- | |<--- DEDUCT ---<--- ACCEPTABLE? --->-----| |
- | | IVE? | |
- | | | | |
- | ---------- | N DON'T KNOW | | |
- | | ACCEPT | | | | |
- | | NOT P | | ----------------- ---------- |
- | ---------- | | CHECK YOU | | ACCEPT | |
- | | | | UNDERSTAND C | | C | |
- | | | ----------------- ---------- |
- | | | | | |
- -->------->-----------------|------------<-------- |
- | |
- |
- |
- IS THERE ANOTHER Y |
- ARGUMENT FOR C OR --->------------|
- FOR NOT C |
- |
- N | ------------ |
- | RECHECK | |
- N Y |ARGUMENTS | |
- -----<------- HAVE YOU ACCEPTED ->--| FOR BOTH |-
- | C AND NOT C ------------
- --------
- | FINISH |
- --------
10. TRUTH, FALSEHOOD, AND EVASION
We have tried to understand something about what makes an argument good or bad. We have seen that for both deductive and non-deductive arguments there are two different issues: when you offer reasons for a conclusion we can examine on the one hand the truth or acceptability of those reasons and on the other hand we can examine the kind of relation, the kind of logical structure, between premises and conclusion. Ordinary people who want to sort out good from bad arguments are in fact concerned with both these separate issues - they want their good arguments both to have true or acceptable premises and to have the appropriate sort of structure; and a failure in either respect is enough to flaw an argument. Part of the difficulty of the subject is to see that the two different respects are quite different; instead of a blanket judgment, we should now be able to make a more precise judgment of an argument. I have concentrated on the questions of structure, especially for deductive arguments, without saying much about truth. I would have preferred to go on like that, since I think that most of the time we have a fairly good idea of what we are getting at, and since people tend to get into tangles when they start talking directly about truth in the abstract. But since this is after all a philosophy course, you may already have started asking yourself awkward questions about truth, and so I shall begin this section with a couple of points about truth as I have been using the notion.
First I shall anticipate a general point to be made later, viz. that the basic notion is not truth, but rather what it is for something (a statement, a belief, a claim, etc.) to be true. The abstract noun "truth" may put obstacles in the way of our understanding that are not there when we think about the verbal phrase "is true". When I say a statement is true, I mean things are as the statement says they are. To begin to find out whether a statement is true, you must first know how it is the statement says things are, i.e. you have to know what it means. The claims a statement makes may be very complex; it may raise several distinct issues; there may then be no simple answer to the question "Is it true?", but the basic idea of truth remains simple - things being as they are said to be.
While I have conceded that sometimes it may not be possible to give a simple straightforward answer to the question "Is that statement true?" I want us to go along with the pretence that we can give a simple answer, and that conversely, there is a simple question of falsehood - if a claim is not true, then it is false, if it is not false it is true. This is perhaps an oversimplification of some of our ordinary ways of thinking and talking. A lot of the time we are satisfied with claims being approximately true: you might agree that Barbados is triangular (i.e. allow that it is true that Barbados is triangular) when in fact Barbados is vaguely triangular, or triangular to a pretty rough approximation. There are other ways in which our distinction between truth and falsehood is not as clean as I am pretending, but I do not think they create any serious problems for us, which is why I shall continue to ignore them.
Another point, and one that is vital for the notion of truth, is that questions of truth or falsehood are absolute and objective questions; they are not to be confused with questions of what or how someone thinks. If I claim that on January 1st, 1983, Jamaica had more than 2 1/2 million people, then either it had or it hadn't - if it had, then what I said is true; if it hadn't, what I said is false - it is of no importance what I happen to think. There is no real sense in pretending that it is 'true for me'. Truth is in general not in the eye, or mind, of the beholder. It goes beyond one's thinking: are things as I think them to be? And it doesn't matter how hard it may be for us to find out.
I must admit that there are cases where it may seem very plausible to try to talk of relative truth, things being true for him, but not for her, etc. These are usually cases where I would suggest that what is being said is pretty complicated, so a straightforward answer is inappropriate: the issues need separating. The simple idea of truth I have introduced is in fact a potent weapon in separating such issues. We may meet a few examples later on where you will be able to see the sort of thing I mean, but unfortunately most of these cases would take us too far from the confines of this course. But as a general warning: if you are tempted to relativize truth, let this make you very suspicious of the issues you are discussing; ask yourself whether there may not be more going on than appears on the surface.
So much for truth in the abstract. Let us recall the simple fact about valid deductive arguments, that they provide a two-edged sword - you can use them to travel from truths to truths, but equally, they transmit falsehood back from the conclusion to the set of premises. And we have already met a simple example of the sort of falsifying strategy that is at the root of much of our learning about the world: you might think that no Muslims eat pork, but there is a Muslim and she is eating pork, so it isn't true that no Muslims eat pork. Many people once thought that all swans are white, but then someone went to Australia and observed that there was a swan and that it was black, so the widespread belief was falsified, was shown to be false by a simple deductive argument.
Some sorts of claim are, then, particularly vulnerable; they take risks, and it is not too difficult to imagine what would make them false. One very important point here is that there is an intuitively obvious sense in which taking such risks is both more interesting and, more importantly, more informative. If I claim that all swans are white, I take a big risk, but I also tell you a lot; if I claim that most swans are white, I still take a risk, but I am beginning to hedge my bets; if I claim that at least a few swans are white, I am risking very little, but equally I am not telling you very much. If I sink to saying only that there may be a white swan or then again there may not, I cannot go wrong, I take no risk at all, but I tell you nothing. The moral is then, if you want to say something, you have to take risks, you have to be prepared to be wrong. Another moral is, if you want to say something it has to be possible to say what it would be like if you were wrong - one way to find out if you really know what someone is saying is to ask what would falsify it; if you can't imagine what would falsify their claims then probably they are not really saying anything.
A third moral, which is partly a matter of tightening up on the previous point, is that it is only worth asking or raising answerable questions. If someone says that 200 angels can stand on a pin, I can imagine 300 standing there; or at least I can use sentences that express that idea. But have I really got any grasp of what would make the original claim true or false? Since there is no possibility of producing evidence one way or the other, the issue is futile, a waste of intellectual energy. "Answerable" does not mean "easily answerable"; I am not recommending that we only ask questions we already know the answers to. But the point is that we must have a sense of what would count as evidence for one answer rather than another.
While these points are, I think, very important, the issue I want us to focus on is rather the outcome of human frailty in the face of them. People want to be informative, so they have to risk being wrong; but equally, people don't like to be wrong, or perhaps to admit to themselves or others that they are wrong. There is obviously a conflict here, but we have worked out what may seem a "solution"; we try to have our cake (acknowledge the falsification) and eat it (keep saying what we started with). But of course we cannot really succeed; unfortunately too many people think they do. Let us look at a very simple example: someone says that no educated person prefers bingo to reading poetry. We then come across John Smith who has a first class degree in classics and writes a regular column on world affairs in a "high-brow" newspaper. We all agree that John Smith is an educated man. We then find out that John Smith prefers bingo to reading poetry. What does our supposed someone say then? "Well, John Smith isn't really educated, you know ..." or he might talk about genuine education, or true education, or education in the proper sense of the word: anything in fact, rather than admit his original claim has been well and truly falsified.
What typically happens in these cases is that you start out with a genuine, informative claim, a claim that, as we have seen, takes risks; but instead of acknowledging that it is too risky, i.e. is wrong, you go on using the same or very similar words to make what is in effect a much weaker, less informative claim, indeed often a claim that is so weak that it cannot go wrong, but which buys such immunity from error by telling us nothing. (We call such safe truths "tautologies"; they are true no matter what the world is like, or true in every possible world, and so in general tell us nothing about what the world actually is like.) The sleight of mind here is effected by using almost the same words, but with very different meanings. In our example, the claim started out with the word "educated" meaning whatever it does in ordinary English, and said that when you picked out people according to that ordinary meaning, you would also find that none of them preferred bingo to reading poetry: that would be a separate matter, to be tested for independently of establishing that they are educated. But after it has been qualified with "real" or "genuine" the word "educated" now involves not preferring bingo to reading poetry as part of its own meaning. Part of what is involved in picking out educated people is now that they do not prefer bingo to reading poetry, so it is hardly news that such educated people do not prefer bingo to reading poetry - it is now as uninformative as "All white swans are white." Here we have come upon a test for informativeness: ask what is involved in picking out Xs, educated people, mentally ill people, etc. If someone says that all Xs are Y, but you find picking out Xs requires already that you determine whether they are Y, then nothing informative is being said. The strategy to watch for is the attempt to evade falsification by using the same or very similar words to say very different things. It looks like the same claim, but in fact it is an empty ghost of the original.
I have attacked one response to falsification, the attempt to pretend nothing has happened. But there is another response that may look similar but which is, in general, perfectly reasonable. Let us return to our swans. We started out with the simple claim that all swans are white; we go to Australia and find some black swans. One simple response we might make is to revise our claim to the slightly more modest claim that all European swans are white. This is still a genuinely informative claim; it hasn't made being white part of what is meant by being a swan or being a European swan, so it still tells us something, it still takes a risk, and for all I know, it may take the right amount of risk. I should also acknowledge that in science we may also do something that is very close to the evasion strategy: we might have said Australian black swans are not really swans at all, they should be re-classified. Now the way we should take this depends on exactly how it is done. Perhaps people might have found some other subtle differences between swans and the black Australian species and begun to use this to distinguish swans from their neighbours. If so, being a swan and being white would remain two distinct issues; we would just have to be rather more careful in identifying swans. But it might have been that colour became crucial, and so being a swan and being white would no longer be distinct issues, and so the meaning of the word "swan" would have changed in such a way that the original claim that all swans are white has become empty. These possibilities indicate for one thing that it is not so much the form of words that matters, but rather what is being said by using them, and that can change both over time and within a couple of sentences. But for our purposes, I think the major point remains how many issues are being raised by what is said: if distinct issues then we have informative claims, if the same issue twice over then we have tautology.
EXERCISE G
1. In the light of the above remarks, what comments would you make on the "true social group" mentioned at the end of the following passage?
Persons do not become a society by living in physical proximity, any more than a man ceases to be socially influenced by being so many feet or miles removed from others. A book or a letter may institute a more intimate association between human beings separated thousands of miles from each other than exist between dwellers under the same roof.... We are compelled to recognize that within even the most social group there are many relations which are not as yet social. A large number of human relationships in any social group are still upon the machine-like plane. Individuals use one another so as to get desired results, without reference to the emotional and intellectual disposition and consent of those used.... So far as the relations of parent and child, teacher and pupil, employer and employee, governor and governed, remain upon this level, they form no true social group, no matter how closely their respective activities touch one another. [33] [Answer.]
2. Can anything be said for the "true self" of the following remark?
When I act against my will, then, it is not my true self doing it, but sin which lives in me. [34] [Answer.]
3. Does the following passage display evasion or a more acceptable strategy?
Agricultural scientists have repeatedly found that maximum productivity of broad-leaved crops occurs when the leaf surface area exposed to the incoming light from above is about 4 or 5 times the surface of the ground.... In a forest the leaf area apparently continues to increase far beyond that limit experimentally shown to increase gross production, since leaf area per ground surface is often 10 or more in an old forest. Since forests are among the most successful of ecosystems with a long geological history of survival, we may well consider the possibility that the extra leaves have other functions in the ecosystem in addition to production of food. [35] [Answer.]
1. Invalid. We suppose there has been an accident; the premises may all be true but the conclusion false - the driver may have fallen asleep, or the steering have gone, or any number of other things may have happened without the brakes failing. It is a very frequent kind of fallacy. If you would like an argument of the same form but about something completely different, try:
- If I know everything I know my own name;
- I know my own name,
- so I know everything.
2. Valid. If you try it with circles, you should get a diagram like this (C = Christians; P = people allowed to eat pork; M = Muslims):
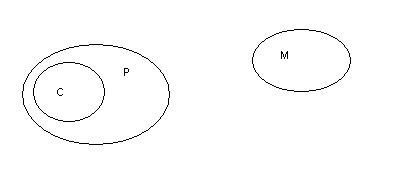
The Cs are inside the Ps, but the Ms are outside the Ps, so there is no way the Cs can touch the Ms.
You could try to produce a contradiction by assuming the falsity of the conclusion: add "Some Christians are Muslims" to the premises, then you can infer that some Muslims are allowed to eat pork, but you already have the claim that no Muslims are allowed to eat pork, and thus you have a contradiction.
If you notice that each component sentence of this argument is different, you might want to say its structure is: p, q, therefore r; and this structure is obviously invalid. What this shows is that the validity of the argument depends on a finer level of structure than just the overall sentences; we have to attend to words like "no" and "some".
3. Invalid. The question of what makes a quantity "absolute" is somewhat involved, but in some sense it has been claimed that accelerations are absolute in a way that velocities, distances and durations may not be. The premises may then be true while the conclusion is false, so the argument is invalid. Without appealing to these perhaps controversial aspects of the interpretation of physics, you could try to find an argument of the same structure which is obviously invalid. For example, Alfred is the grandson of Deirdre and Tom; Alfred is an alcoholic, so Deirdre and Tom are alcoholics. The danger with such a counter-example is that it overlooks some peculiarity of "being the second derivative of". But one way to express any such peculiarities would be to say the argument assumes something like "All properties of second derivatives are shared by the properties they derive from." With such an additional premise the argument becomes valid, but the additional premise is highly implausible.
4. Invalid. This, like (1), is a frequent fallacy. To illustrate with the same substitutions: if I know everything I know my own name, so if I don't know everything I don't know my own name.
The basic structures related to these fallacies are:
- (i) If p then q, q, therefore p (this is (1) above)
- (ii) If p then q, not p, therefore not q (this is close to the present example - why is it not the same?).
Both these patterns are fallacious. There are two valid deductive arguments with the following patterns:
- (iii) If p then q, p, therefore q (this is often called "modus ponens")
- (iv) If p then q, not q, therefore not p (often called "modus tollens").
These patterns are of fundamental importance, and it is worth effort seeing what exactly is going on.
5. Valid. This is a famous specimen argument which cannot obviously be handled with the circles. Note also the premise leaves unstated how many horses are animals: obviously all are, and that is what the argument requires. But this way of using language allows a certain amount of uncertainty in some cases and you should be on guard for such usage. If the argument is not intuitively obvious, you could assume the opposite of the conclusion, there is at least one horse's head that is not an animal's head, from which you can infer that there is at least one horse which is not an animal, which contradicts the given premise that all horses are animals; so this premise rules out the opposite of the given conclusion, so that it rules in the conclusion, i.e. the argument is valid.
6. Invalid. It is modelled on some remarks of Thomas Aquinas in his five attempted proofs of the existence of God. The words which tell us how many are called "quantifiers" in logic, and this kind of fallacy is due to a fallacious quantifier shift. The premise says: for each thing, there is at least one time when it doesn't exist; the conclusion switches the order of the quantifiers: there is at least one time when for each thing, it doesn't exist. A simple example to help you remember the error is: all roads lead somewhere, so there is one place to which all roads lead.
7. Invalid. It is not so easy to "see" this fact just by thinking about the premises and the conclusion - in fact one of the many reasons for studying Geach's Reason and Argument is to learn a simple way of treating such arguments with the help of diagrams and some simple maths. The basic idea is to take "Most As are B" as saying there are more As that are B than there are As that are not B, and then, with the help of a diagram, to find sets of numbers which validate or invalidate a given argument. In the present case, one counter-example to the argument would be a world in which there are 16 Swedes, 9 Protestant and 7 non-Protestant; 6 non-Protestant Swedes visit Lourdes as against 2 Protestant; so exactly half of the Swedes visit Lourdes. In such a world, the premises are all true, the conclusion false, so the argument is invalid.
1. It may be true that a society requires more than physical proximity; it requires persons to enter into relations with each other. But our ordinary understanding of a social group or a society merely requires these sorts of relationship, it does not require the special caring and respectful relationships the author obviously prefers. "True" is here simply serving to say "the sort of social group I prefer"; it is probably an attempt to gain support for views without much argument since we have to acknowledge the importance and pervasiveness of ordinary social groups; by trying to re-define "social" the author will then try to use these admissions to support his re-defined relationships.
2. Again the most likely account here is that "true" means preferred; those actions I regret are shuffled off me on to the "sin which lives in me". Or on to a "lower" self. In general there is little else to support such a bifurcation of one's self, so it is probably an unjustified cheat. But the self is somewhat mysterious and complicated, so there might be occasions when this kind of distinguishing can be justified (actions which for that person are very rare and felt as intrusions from outside his working everyday self might reasonably be denied to that person's "true self"; or again actions produced by hypnotic suggestion or various other actual or possible means).
3. The evidence presented falsifies the claim that the only function of leaves is to produce food as efficiently as possible. But instead of using this to falsify the general principle that natural features of organisms are to be explained by reference to their contribution to the survival of the species, the principle is used to argue that there must be other functions for leaves besides food production. This is not yet to evade falsification, since it opens up a search for other functions: one would approach evasion if no such other functions were found and one continued to insist that there had to be other functions.
URL http://www.uwichill.edu.bb/bnccde/epb/aa7-10.html
HTML prepared June 2000, last revised June 29th, 2000.